Este blog será usado como "Caderno Coletivo Virtual" para os alunos do 9º ano A da Escola SESI de Pederneiras.
quinta-feira, 30 de outubro de 2014
Diagonal do Quadrado e Altura do Triângulo Equilátero
- Diagonal do Quadrado:
-Altura do Triângulo Equilátero:
sexta-feira, 24 de outubro de 2014
TRIÂNGULO RETÂNGULO.
•O que é um triângulo retângulo?
É um triângulo que possui um ângulo de 90º ( ângulo reto) e seus determinados "lados" são chamados de:
•O triângulo retângulo e suas relações métricas:
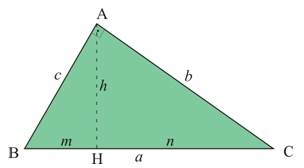
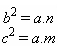
- O produto dos catetos é igual ao produto da hipotenusa pela altura relativa à hipotenusa.
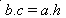
- O quadrado da altura é igual ao produto das projeções dos catetos sobre a hipotenusa.
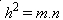
- O quadrado da hipotenusa é igual à soma do quadrado dos catetos(teorema de Pitágoras).
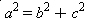
segunda-feira, 15 de setembro de 2014
Altura do Triângulo
Bom já sabemos alguns elementos básicos sobre um triângulo como: Vértices, lados e ângulos.
MÉTODO DE CONSTRUÇÃO DA ALTURA DO TRIÂNGULO
1 – Tracemos um triângulo ABC qualquer.
2 – Vamos construir a altura relativa ao vértice A. Portanto, pela definição de altura, ela tem que passar pelo ponto A e ser perpendicular à reta suporte do lado oposto, ou seja, à reta BC.
3 – Vamos pegar o compasso e, colocando a ponta seca no ponto A, traçar um arco que corte a reta BC em dois pontos D e E.
4 – Agora, com uma abertura do compasso maior que a metade do arco DE, colocando-se a ponta seca em D, traçamos um pequeno arco acima da reta BC.
5 – Com a ponta seca em E, mantendo a mesma abertura, traçamos outro pequeno arco de modo que intersecte o arco anterior. Dessa maneira, achamos o ponto F.
6 – Ao unirmos o ponto A com o ponto F, determinamos uma reta que é perpendicular àreta BC e que passa pelo ponto A.
7 – O segmento de reta AH é a altura relativa ao vértice A que queríamos.
8 – Para traçar as outras alturas, relativas aos vértices B e C, procede-se de maneira análoga.
Link das informações acima:
http://www.sofazquemsabe.com/2013/07/altura-triangulo-construcao-geometrica-ceviana-notavel-especial.html?m=1
Bissetriz e Incentro.
Bissetriz
- Como construir a bissetriz:
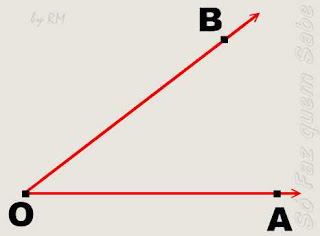
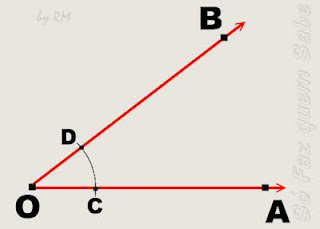
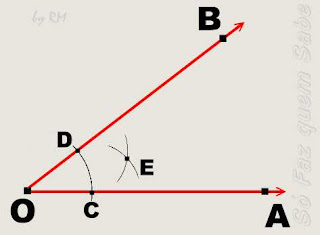
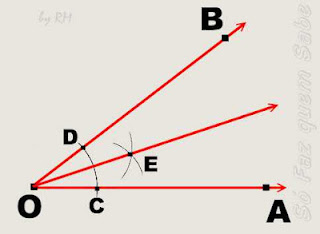
Incentro
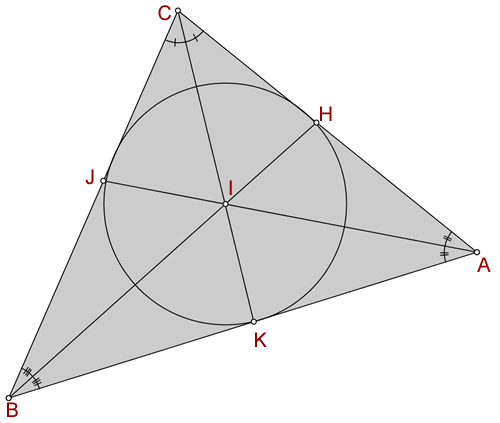
Mediana
O encontro das medianas no triângulo se encontra o Baricentro, que é o ponto de equilíbrio.
Baricentro de um triângulo
domingo, 14 de setembro de 2014
Dividindo o segmento em partes iguais
quinta-feira, 5 de junho de 2014
Equações do 2º grau: Método do Discriminante


quarta-feira, 4 de junho de 2014
Metodo de completar o quadrado
terça-feira, 3 de junho de 2014
Fator Comum em Evidência
Exemplo:
ax+bx+cx
Obs:Fator comum em evidência "x".
Atenção:quando você encontra o fator comum,coloque ele em evidência e divide ele por todos os outros números.
Coeficientes da equação
sexta-feira, 30 de maio de 2014
Equações do 2º grau: Método do Discriminante
Δ= (-6)² - 4*1*8
sábado, 17 de maio de 2014
Fator Comum em Evidência
Na fatoração por fator comum em evidência, utilizamos a idéia de fazer grupos de polinômios, ao fatorar escrevemos a expressão na forma de produto deexpressões mais simples.
O polinômio x² + 2x possui forma fatorada, veja:
x² + 2x .: podemos dizer que o monômio x é comum a todos os termos, então vamos colocá-lo em evidência e dividir cada termo do polinômio x² + 2x por x.
Temos: x (x + 2)
Concluímos que x (x + 2) é a forma fatorada do polinômio x² + 2x.
Para termos certeza dos cálculos, podemos aplicar a distribuição na expressão x (x + 2) voltando ao polinômio x² + 2x.
Exemplos de fatoração utilizando fator comum em evidência:
Exemplo 1
8x³ - 2x² + 6x (fator comum: 2x)
2x (4x² - x + 3)
Exemplo 2
a6 – 4a² (fator comum: a²)a² (a4 – 4)
Exemplo 3
4x³ + 2x² + 6x (notamos que o monômio 2x é comum a todos os termos)
2x (2x² + x + 3)
Exemplo 4
6x³y³ – 9x²y + 15xy² (fator comum: 3xy)
3xy (2x²y² – 3x + 5y)
Exemplo 5
8b4 – 16b² – 24b (fator comum: 8b)
8b (b³ – 2b – 3)
Exemplo 6
8x² – 32x – 24 (fator comum: 8)
8 (x² – 4x – 3)
Exemplo 7
3x² – 9xy + 6x + 21x3(fator comum: 3x)
3x (x – 3y + 2 + 7x2)
Exemplo 8
5a²b³c4 + 15 abc + 50a4bc2 (fator comum: 5abc)
5abc (ab²c³ + 3 + 10a3c)
Por Marcos Noé
segunda-feira, 28 de abril de 2014
como identificar equaçoes de 2º grau

2x + 1 = 0, o expoente da incógnita x é igual a 1. Dessa forma, essa equação é classificada como do 1º grau.
2x² + 2x + 6 = 0, temos duas incógnitas x nessa equação, em que uma delas possui o maior expoente, determinado por 2. Essa equação é classificada como do 2º grau.
quarta-feira, 2 de abril de 2014
Funções do 1° Grau
 Função Crescente(Grandeza diretamente proporcionais)
Função Crescente(Grandeza diretamente proporcionais).jpg) Função decrescente (Grandeza inversamente proporcionais )
Função decrescente (Grandeza inversamente proporcionais )
segunda-feira, 31 de março de 2014
Exercício
Obs: Tente resolver sem olhar nas respostas.
Em uma indústria metalúrgica o custo de produção de uma peça automotiva corresponde a um custo fixo mensal de R$ 5 000,00 acrescido de um custo variável de R$ 55,00 por unidade produzida mais 25% de impostos sobre o custo variável. Considerando que o preço de venda dessa peça pela indústria aos comerciantes é de R$ 102,00, determine:
a) a função custo da produção de x peças.
b) a função receita referente a venda de x peças.
c) a função lucro na venda de x peças.
d) o lucro obtido com a venda de 500 unidades.
RESPOSTAS:
a) A função custo será dada pela somatória do custo fixo, do custo variável e do imposto cobrado de acordo com o custo variável.
Custo = 5000 + 55x + 0,25 * 55x
b) A função receita é dada por:
Receita = 102x
c) A função lucro é obtida subtraindo a função receita da função custo.
Lucro = 102x – (5000 + 55x + 0,25 * 55x)
Lucro = 102x – 5000 – 55x – 0,25 * 55x
Lucro = 102x – 55x – 13,75x – 5000
Lucro = 33,25x – 5000
Quando calculamos a função lucro determinamos uma expressão capaz de determinar o lucro líquido obtido da venda de x peças, isto descontados os custos de produção e os impostos municipais, estaduais e federais.
d) O lucro obtido com a venda de 500 unidades corresponde a:
f(x) = 33,25x – 5000
f(500) = 33,25 * 500 – 5000
f(500) = 16 625 – 5000
f(500) = 11 625
O lucro obtido é igual a R$ 11 625,00.
FONTE:Brasil Escola.
Vídeo sobre funções do 1º grau, representadas graficamente
sexta-feira, 28 de março de 2014
uma judiinha pro trabalho de portugues pesoal!
-
- Já me decidi: só irei à praia, se antes eu comprar um protetor solar. (Período Composto).
2. Irei à praia.
São orações coordenadas entre si e que não são ligadas através de nenhum conectivo. Estão apenas justapostas.
Ao contrário da anterior, são orações coordenadas entre si, mas que são ligadas através de uma conjunção coordenativa. Esse caráter vai trazer para esse tipo de oração uma classificação:
- Nem comprei o protetor solar, nem fui à praia.
- Comprei o protetor solar e fui à praia.
- Ainda que a noite acabasse, nós continuaríamos dançando.
- Não comprei o protetor solar, mas mesmo assim fui à praia.
- Ora sei que carreira seguir, ora penso em várias carreiras diferentes.
- Quer eu durma quer eu fique acordado, ficarei no quarto.
- Conclui o meu projeto, logo posso descansar.
- Tomou muito sol, consequentemente ficou adoentada.
- Só fiquei triste por você não ter viajado comigo.
- Não fui à praia pois queria descansar durante o Domingo.



.jpg)



.JPG)


